
أثبت أن ( جـ ََ)^2 = ( ب َ )^2 + ( أ َ )^2 – 2 أ َ بَ حتا حـ
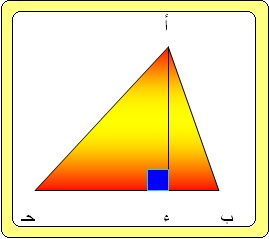
فى المثلث أ ب ء قائم فى ء
(أ ب)^2 = (أ ء )^2 + (ب ء) ^2 (1)
ولكن بء = ب حـ - ء حـ بتربيع الطرفين
(ب ء )^2 = (ب حـ ) ^2+ (ء حـ) ^2- 2 ( حـ ء ) ( ب حـ) (2)
بالتعويض بـ 2 فى 1
(أ ب)^2 = (أ ء )^2 +(ب حـ ) ^2+ (ء حـ) ^2- 2 ( حـ ء ) ( ب حـ) (3)
ولكن فى المثلث أ ء جـ قائم فى ء
(أء)^2 = (أ حـ)^2 – ( ء حـ)^2 (4)
بالتعويض بـ 4 فى 3
(أ ب)^2 = (أ حـ)^2 – ( ء حـ)^2 +(ب حـ ) ^2+ (ء حـ) ^2- 2 ( حـ ء ) ( ب حـ)
(أ ب)^2 = (أ حـ)^2 +(ب حـ ) ^2- 2 ( حـ ء ) ( ب حـ) (5)
ولكن فى المثلث أ ء جـ قائم فى ء
حـ ء= أحـ حتا حـ
(أ ب)^2 = (أ حـ)^2 +(ب حـ ) ^2- 2 ( ب حـ) ( أ حـ ) حتا حـ
اذا ( جـ ََ)^2 = ( ب َ )^2 + ( أ َ )^2 – 2 أ ب َ حتا حـ
مماسق نستنتج أ ن
(1) (أ َ)^2 = (ب َ)^2 + ( حـَ)^2 - 2(بَ) (حـَ) حتا أ
(2) (ب َ)^2 = (أ َ)^2 + ( حـَ)^2 - 2( أ َ)( حـَ) حتا ب
(3)(حـَ)^2= ( أ َ )^2 + ( بَ)^2 - 2( أ َ) ( ب َ) حتا حـ
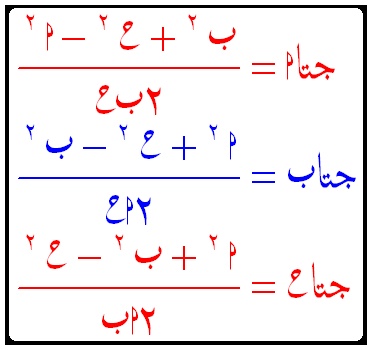
يستخدم قانون حيب تمام الزاوية فى الحالات الاتية
(1) إذا علم أطوال أضلاع المثلث الثلاثة
(2) إذا علم طول ضلعين فى المثلث وقياس الزاوية المحصورة بينهما
